Les portes logiques

Objectifs: Codage d'une information par une variable à deux états et opérations utilisant de telles variables.

Matériel: plaques de circuit imprimé pouvant recevoir un circuit intégré de 16 bornes maximum et équipé de bornes pour brancher des fils de connexion.
Circuits intégrés à 4 portes logiques : 74 HC 00, 74 HC 08, 74 HC 32, 74 HC 86.

I Niveaux logiques

On a vu qu'une information pouvait être codée par un nombre.

Un caractère peut être codé par un nombre entre 0 et 255 (code ASCII).

Ainsi, la lettre M (majuscule) est codée par le nombre 77.

L'informatique n'utilisant que deux états, on n'utilise que les chiffres 0 et 1. C'est la numération binaire.

Un nombre de huit chiffres binaires (8 bits) est un octet.

1) Convertir en numération décimale l'octet ci-contre.

Pour transmettre l'information codée, on peut utiliser:

un potentiel
0 V correspond au bit 0,
5 V (par ex) correspond au bit 1.
la lumière: CD et CDrom.
l'infra-rouge: télécommande.

L'état logique 0 est dit niveau bas.
L'état logique 1 est dit niveau haut.

Transmission de la lettre M par une tension:

le port série transmet un signal électrique ayant cet aspect.

La rapidité de transmission des informations dépend des performances de l'ordinateur.

2) Un octet est nécessaire pour coder jusqu'à 256 états.
Combien de bits faut-il pour coder 16 couleurs?

3) Donner l'aspect de la tension qui permet de transmettre l'octet 85.

II Notion de fonction logique

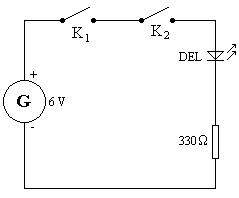
Le circuit électrique ci-contre permettent de comprendre aisément ce qu’est une fonction logique.

Les interrupteurs K₁ et K₂ représentent les variables logiques d'entrée E₁et E₂:

K₁ouvert: E₁= 0,
K₁fermé: E₂= 1.

La diode électroluminescente (DEL) représente la variable logique de sortie S:

DEL éteinte: S = 0,
DEL allumée: S = 1.

1) Remplir un tableau comme ci-contre, appelé table de vérité.

_{Table de vérité 1}
E₁	E₂	S
0	0
0	1
1	0
1	1

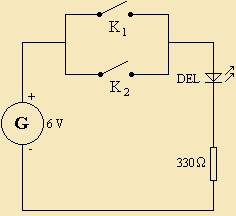
2) Compléter la table de vérité ci-contre.

3) Justifier les dénominations:

fonction "ET" pour la fonction représentée par la table de vérité N°1,
fonction "OU" pour la fonction représentée par la table de vérité N°2.

_{Table de vérité 2}
E₁	E₂	S
0	0
0	1
1	0
1	1

III Etude de quelques portes logiques

A) Circuits intégrés

Les circuits intégrés utilisés possèdent 14 bornes numérotées

2 bornes pour l’alimentation N^os 7 et 14,
3 pour chacune des 4 portes logiques.

Chaque porte logique a deux entrées (notées E) et permet donc de réaliser une fonction logique à deux variables logiques comme par exemple les fonctions logiques "ET" et "OU" vues précédemment.

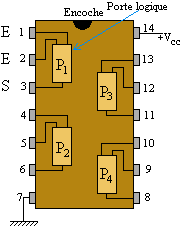On rappelle que tout circuit intégré doit d'abord être alimenté. Il ne peut fonctionner sans alimentation.

1) Quelles sont les bornes utilisées pour tester la porte logique N° 1?

B) Rôle d'une porte logique

Une porte logique permet, à partir de variables logiques d'entrée, de déterminer une variable logique de sortie.

Ci-contre la représentation symbolique d'une porte logique "ET".

C) Reconnaissance des fonctions logiques

Dans un premier temps, on se propose de reconnaître les fonctions logiques réalisées par différents circuits intégrés de références:

74 HC 00
74 HC 08
74 HC 32
74 HC 86

On testera une des portes logiques de chacun de ces circuits intégrés.

tests.gif (2206 octets)

Réaliser le montage ci-dessus avec le plus grand soin. Alimenter le circuit intégré. Puis imposer aux entrées des tensions hautes ou basses correspondant respectivement aux états logiques 0 et 1.
2) Reproduire ce schéma lorsque les deux entrées sont au niveau logique 1.

L’état logique de la sortie sera connu grâce à la DEL et peut être confirmé par un voltmètre.

On remplira une table de vérité pour chacun des circuits intégrés testés.

E₁	E₂	S
0	0
0	1
1	0
1	1

3) Identifier ces portes logiques d'après les tables de vérité ci-après.

Porte "ET"

E₁	E₂	S
0	0	0
0	1	0
1	0	0
1	1	1

Porte "OU"

E₁	E₂	S
0	0	0
0	1	1
1	0	1
1	1	1

Porte "NON ET"

E₁	E₂	S
0	0	1
0	1	1
1	0	1
1	1	0

Porte "NON OU"

E₁	E₂	S
0	0	1
0	1	0
1	0	0
1	1	0

"OU EXCLUSIF"

E₁	E₂	S
0	0	0
0	1	1
1	0	1
1	1	0

Les schémas conventionnels des portes logiques sont donnés ci-après.

NON ET

NON OU

OU EXCLUSIF

IV L'additionneur binaire

A) Addition de deux nombres à 1 chiffre

1) Compléter cette table d'addition en donnant le résultat sous forme d'un nombre à deux chiffres.

2) Les colonnes retenue et unité correspondent respectivement aux résultats de deux tables logiques. Lesquelles?

Addition				Somme
Nombre 1		Nombre 2		Retenue	Unité
0	+	0	=	0	0
0	+	1	=
1	+	0	=
1	+	1	=

B) Addition binaire utilisant deux portes logiques

3) Réaliser le montage cicontre à l'aide des deux portes logiques bien choisies (réponse 2).

4) Vérifier que l'on obtient la table d'addition ci-dessus en mettant les deux entrées aux états logiques convenables.

add_bin.gif (2562 octets)

V Réalisation de portes logiques par association de plusieurs portes logiques

A) Porte "NON"
1) Relier entre elles les deux entrées d'une porte "NON ET". Remplir sa table de vérité après l'avoir testée.

E	S

2) Justifier le nom de cette porte. Schéma conventionnel:

p_non.gif (1917 octets)

B1) Association de deux portes logiques

Réaliser les connections indiquées ci-contre en contrôlant bien les numéros des entrées connectées.
Vérifier avant de mettre sous tension.

3) Quelle porte logique a-t-on réalisée?

E₁	E₂	S₁	S

assoc2.gif (2294 octets)

B2) Association de trois portes

Réaliser les connections indiquées ci-contre et construire la table de vérité de cette association.

4) Quelle porte logique a-t-on réalisée?

E₁	E₂	S₁	S₂	S

assoc3.gif (2535 octets)

C) Exercice

Sans réaliser le montage ci-contre, remplir la table de vérité de l'ensemble et identifier la porte ainsi réalisée.

E₁	E₂	S₁	S₂	S₃	S
0	0
0	1
1	0
1	1

assoc4.gif (2560 octets)

Remarque: Toutes les portes logiques peuvent être réalisées à partir d'associations de portes "NON ET".

En conclusion, on retiendra que les portes logiques permettent de réaliser des opérations élémentaires. Nos calculatrices utilisent, de manière très élaborée, les mêmes principes de calcul.

Circuit imprimé et son circuit intégré à 14 pattes.